| 4 | 5 | 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 1 | 3 | 7 | |||||
| 9 | ||||||||
| 5 | 4 | 7 | ||||||
| 3 | 1 | 8 | ||||||
| 6 | 5 | 2 | ||||||
| 7 | ||||||||
| 2 | 1 | 6 | 9 | |||||
| 8 | 7 | 3 |
Math and Logic Puzzles: Redux
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Bringing back the sudoku puzzles:
STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Mitillos
-
Mitillos HeMafia Scum
- Mitillos
He- Mafia Scum
- Mafia Scum
- Posts: 2300
- Joined: August 23, 2012
- Pronoun: He
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Sudoku is good STRANGERCOUG: Stranger Than You!
STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Scigatt
-
Scigatt Goon
- Scigatt
- Goon
- Goon
- Posts: 833
- Joined: January 4, 2008
- Location: Vancouver, Canada
- Mitillos
-
Mitillos HeMafia Scum
- Mitillos
He- Mafia Scum
- Mafia Scum
- Posts: 2300
- Joined: August 23, 2012
- Pronoun: He
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Here's a more challenging sudoku I came up with that should be visually interesting as well:
6 8 4 7 9 1 3 8 5 6 8 9 1 4 2 6 2 6 7 4 7 4 5 3 4 2 1 7 9 STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Mitillos
-
Mitillos HeMafia Scum
- Mitillos
He- Mafia Scum
- Mafia Scum
- Posts: 2300
- Joined: August 23, 2012
- Pronoun: He
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Correct STRANGERCOUG: Stranger Than You!
STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
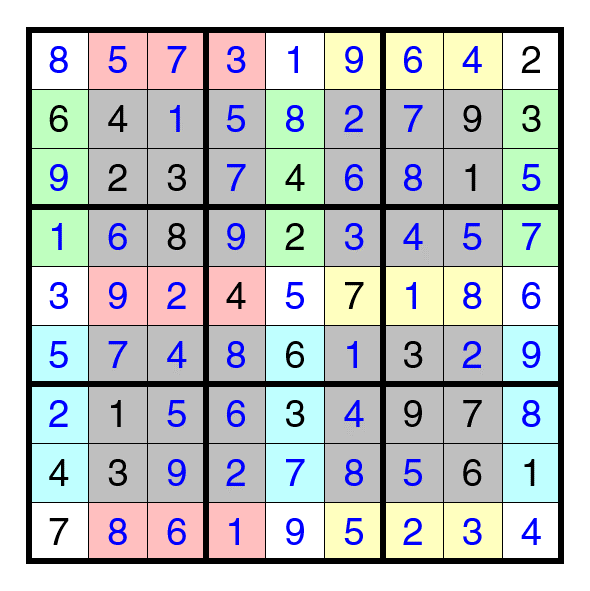
Here's another fun sudoku one, and this one is part one of a two-parter:
The below is a hyper sudoku puzzle, also known as a "windoku" puzzle. The standard rules apply except with one additional restraint: four "window panes", partly overlapping each of the nine boxes, are shaded gray, and each pane must also have the digits from 1 to 9 exactly once. Here is the puzzle:

Part 1, as in my last two questions, is to solve the windoku puzzle. Part 2 will be posted when the correct solution is posted.STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Mitillos
-
Mitillos HeMafia Scum
- Mitillos
He- Mafia Scum
- Mafia Scum
- Posts: 2300
- Joined: August 23, 2012
- Pronoun: He
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Very good Now...
Now...
Spoiler: Part twoSTRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Mitillos
-
Mitillos HeMafia Scum
- Mitillos
He- Mafia Scum
- Mafia Scum
- Posts: 2300
- Joined: August 23, 2012
- Pronoun: He
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Looks good to me STRANGERCOUG: Stranger Than You!
STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- word321
-
word321 Mafia Scum
- word321
- Mafia Scum
- Mafia Scum
- Posts: 1305
- Joined: March 18, 2020
hmm
Ill try to keep alive this section
I guess a lot of different ppl come to this thread, so here is one constructive in nature that can (supposedly) be enjoyed by ppl with different degrees of knowledge; it also serves as basis to expand ur knowledge of math while we r at it (if u didnt know about it already)!
To solve this u will need basic algebra (think about working with the x and decomposing a number in prime factors) and know about sum and multiplication.
So first lets begin with an operation:Module.
We will write the module operation between 2 numbers x and y with the symbol % (x%y) and read it as "x module y".
The intuition behind module is the remainder of an integer division; 9%2=1, for example, because 9/2= 8/2+1/2; 8/2=4, but 1 is left as a remainder, as it can not be divided by 2 into an integer number.
Formally, we say that p%q=r if and only if there exists an integer n such as p=n*q+r, with r>=0 and r<q.
U can prove it if u want, but it is not necessary, that the operation is well defined and whatever formality nitpicks u have.
Modules generalize a lot of the concepts we work with, and we use that operation constantly, even if we dnt realize it. Want an example? Lets say it is 5:30 Pm; wich minute well have in 92 minutes? Those quick at calculating stuff will now it will be 7:02; it is 60+30+2 +the initial 30, rendering 60+60+2. The answer to wich minute is it is the answer to (30+92)%60; with hours, it works the same way. if it is 23:00, in 48 hours it will be 23:00, and in 5 hours it will be 4:00; that is a module by 24.
so, lets go to the challenges:
1. Prove that % is distributed over addition, that is:
(x+y)%z=(x%z+y%z)%z
Examples:
(5%3+11%3)%3=(2+2)%3=1=(5+11)%3
Hint:
Spoiler:
2. Prove that the sum of 2 numbers is even if and only if both numers are even or both numbers are odd
Hint:
Spoiler:
3. Prove that the same thing above occurs with multiplication:
(x*y)%z=(x%z*y%z)%z
Example:
(7%3)*(11%3)%3=(1*2)%3=2=(7*11)%3=77%3 (75=3*25)
Hint:
Spoiler:
Now comes the FUN stuff! Well, if u r stilll with me it must mean u r having fun, right? Right? Well, if u r:
Remember those tricks we used when we were learning the multiplicaction table and what nots? now well prove some of them:
4. Prove that a number is a multiple of 2 if the last digit is a multiple of 2, and that a number is multiple of 5 if the last digit is 0 or 5.
Hint:
Spoiler:
5. Prove that a number is multiple of 3 if the sum of its digits is a multiple of 3
Hint:
Spoiler:
6. What is the last digit of 7^49?
Hint:
Spoiler:
So there it is! The idea was to be doable by a lot of ppl (hopefully), and at the same time answering some of the mysteries we might have had on the school. Remember to spoiler ur answers, and leave more puzzles/exercises/challenges!Last edited by word321 on Mon Jul 27, 2020 1:27 pm, edited 1 time in total.Played inNewbie 1992,Newbie 1997,Newbie 1999,Large Normal 227,Newbie 2006,Open 784,Open 787,Newbie 2019, Open 790, Newbie 2022.
Currently playing in Open 794, Newbie2028.
Currently UTC-3.- Ircher
-
Ircher He / Him / HisWhat A Grand Idea
- Ircher
He / Him / His- What A Grand Idea
- What A Grand Idea
- Posts: 15190
- Joined: November 9, 2015
- Pronoun: He / Him / His
- Location: CST/CDT
In post 138, word321 wrote:1. Prove that % is distributed over addition, that is:
(x+y)%z=(x%z+y%z)%zSpoiler: My Solution
I will note that #2 is much easier to do by directly applying the definitions of even and odd versus using the module operation.Last edited by Ircher on Sat Sep 19, 2020 1:17 pm, edited 2 times in total.- word321
-
word321 Mafia Scum
- word321
- Mafia Scum
- Mafia Scum
- Posts: 1305
- Joined: March 18, 2020
the solution is correct!
and u r right, it is "easy" to prove 2 by hand; but I blv it is more of an issue with notation. The core principle of doing it directly and using the % notation is the same, calling the same thing with different names; but I left it there just to illustrate the logic to be used in further demostrations (so ppl can "adapt" to "adding things module something").Played inNewbie 1992,Newbie 1997,Newbie 1999,Large Normal 227,Newbie 2006,Open 784,Open 787,Newbie 2019, Open 790, Newbie 2022.
Currently playing in Open 794, Newbie2028.
Currently UTC-3.- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Let z1 and z2 be two complex numbers whose magnitudes are r1 and r2 respectively and whose phases are φ1 and φ2 respectively. Prove algebraically that z1z2 = r1r2 cis(φ1 + φ2), where cis(φ) = cos(φ) + i sin(φ).STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- D3f3nd3r
-
D3f3nd3r he/himBest Social Game

- D3f3nd3r
he/him- Best Social Game

- Best Social Game

- Posts: 1367
- Joined: March 25, 2012
- Pronoun: he/him
- Location: Maryland
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
I will understand you if you use j. Thanks for the heads up.STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- D3f3nd3r
-
D3f3nd3r he/himBest Social Game

- D3f3nd3r
he/him- Best Social Game

- Best Social Game

- Posts: 1367
- Joined: March 25, 2012
- Pronoun: he/him
- Location: Maryland
- Contact:
- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
In post 141, StrangerCoug wrote:Let z1 and z2 be two complex numbers whose magnitudes are r1 and r2 respectively and whose phases are φ1 and φ2 respectively. Prove algebraically that z1z2 = r1r2 cis(φ1 + φ2), where cis(φ) = cos(φ) + i sin(φ).Spoiler: HintSTRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Ircher
-
Ircher He / Him / HisWhat A Grand Idea
- Ircher
He / Him / His- What A Grand Idea
- What A Grand Idea
- Posts: 15190
- Joined: November 9, 2015
- Pronoun: He / Him / His
- Location: CST/CDT
In post 141, StrangerCoug wrote:Let z1 and z2 be two complex numbers whose magnitudes are r1 and r2 respectively and whose phases are φ1 and φ2 respectively. Prove algebraically that z1z2 = r1r2 cis(φ1 + φ2), where cis(φ) = cos(φ) + i sin(φ).Spoiler: My Attempt- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Spoiler: Response to Ircher's attemptSTRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress.- Ircher
-
Ircher He / Him / HisWhat A Grand Idea
- Ircher
He / Him / His- What A Grand Idea
- What A Grand Idea
- Posts: 15190
- Joined: November 9, 2015
- Pronoun: He / Him / His
- Location: CST/CDT
Spoiler:- StrangerCoug
-
StrangerCoug He/HimDoes not Compute
- StrangerCoug
He/Him- Does not Compute
- Does not Compute
- Posts: 12457
- Joined: May 6, 2008
- Pronoun: He/Him
- Location: San Antonio, Texas
- Contact:
Spoiler:STRANGERCOUG: Stranger Than You!
Current avatar by PurryFurry of FurAffinity.
What Were You Thinking XV! is in progress. - StrangerCoug
Copyright © MafiaScum. All rights reserved.
- Ircher
- StrangerCoug
- Ircher
- StrangerCoug
- D3f3nd3r
- StrangerCoug
- D3f3nd3r
- StrangerCoug
- word321
- Ircher
- word321
- StrangerCoug
- Mitillos
- StrangerCoug
- Mitillos
- StrangerCoug
- StrangerCoug
- Mitillos
- StrangerCoug
- Mitillos
- Scigatt
- StrangerCoug
- Mitillos
- StrangerCoug